B) Geometrische Darstellung und Berechnung
I. Grundlagen
II. Erwartete Neigung der Mondsichel
III. Sichtbare Neigung der Mondsichel
IV. Mondphase
V. Internet
VI. Mondneigung und Mondbahn
I. Grundlagen

1.) Ein Gestirn, auch Mond und Sonne, sieht man - wie Bild 1 zeigt - in einer auf dem Kompass abzulesenden Himmelsrichtung (Azimut) und unter einem Höhe genannten und mit dem Sextanten zu messenden Winkel (α). Die Entfernung spielt dabei keine Rolle. Die Höhe wird, anders als früher in der nautischen Navigation, nicht im Verhältnis zur Kimm (der sichtbare Horizont auf dem Meer) gemessen, sondern im Verhältnis zum idealen Horizont, also zu der Ebene, die vom Lot senkrecht durchstoßen wird.
2.) Die Sichel ist der Teil der Mondoberfläche, der sowohl von der Erde aus sichtbar als auch von der Sonne beleuchtet ist. Dabei soll hier auch dann von der "Sichel" gesprochen werden, wenn der Mond mehr als halb voll ist. Die Grenze zwischen dem sichtbaren und dem unsichtbaren Teil der Mondoberfläche ist der Kreis, den die Berührungspunkte der vom Auge zur Mondkugel gehenden Tangenten auf der Kugeloberfläche bilden. Ist man - wie beim Mond - genügend weit entfernt, nähert sich der Kreis einem Großkreis (der „Blick-Großkreis“), der die Kugel in zwei gleich große Hälften teilt und auf dessen Ebene die Verbindungslinie zwischen dem auf den Mond gerichteten Auge und dem Mondmittelpunkt senkrecht steht („Blickachse“). Die Grenze zwischen dem beleuchteten und dem dunklen Teil der Mondoberfläche ist der Großkreis, den die Berührungspunkte der von der Sonne zum Mond gehenden Tangenten auf dessen Oberfläche bilden („Sonnen-Großkreis“, Terminator). Auf dessen Ebene steht die Symmetrieachse der beleuchteten Mondhälfte, d. i. die Verbindung zwischen Mondmittelpunkt und Sonne senkrecht. Die Spitzen der Mondsichel befinden sich dort, wo sich „Blick-Großkreis“ und „Sonnen-Großkreis“ schneiden. Weiter unten in Bild 5 sind die Details zu sehen.
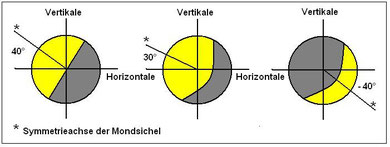
3.) Manchmal steht die Mondsichel aufrecht, zumeist ist sie nach der einen oder der anderen Seite geneigt (siehe Bild 2). Das ist die "sichtbare" Mondneigung. Sie erkennt man mit dem direkt auf den Mond gerichteten Blick. Wandert der Blick zur Seite, ist der Mond am Rand des Sichtfelds evtl. noch bemerkbar. Irgendwelche Einzelheiten, darunter die Neigung der Sichel, werden aber nicht mehr wahrgenommen. Also muss man den Mond direkt ansehen, um die Sichelneigung beurteilen zu können. Die Beispiele in Bild 2 zeigen links eine Mondsichel, die mit einem Winkel von 40° nach links oben geneigt ist und augenscheinlich von links oben beschienen wird, weswegen man den Schluss zieht, die Sonne müsse höher stehen als der Mond, tiefer dagegen im Fall der rechts abgebildeten, ersichtlich von rechts unten beleuchteten Sichel. Die Neigung der Mondsichel wird beurteilt, indem man das Lot bzw. die Horizontale (gedanklich) vor das Auge hält und darüber hinweg auf den Mond schaut (Mondscheibe mit „Fadenkreuz“). Die Mondneigung ist der Winkel, den die auf den Mond projizierte Horizontale und die Symmetrieachse der Sichel einschließen, und kann geometrisch und rechnerisch dargestellt sowie mit einem geeigneten Gerät gemessen werden.
4.) Die Sonne ist mit durchschnittlich rd. 150 Mio km fast 400-mal so weit von der Erde entfernt wie der Mond mit durchschnittlich rd. 384.000 km. Die Sonnenstrahlen, die auf Mond und Erde treffen, haben zueinander einen Winkel von 0° bis 0,15° und können als parallel angesehen werden. Sie treffen auf Mond und Erde aus der nahezu gleichen Richtung. Und die Sonne kann ohne Fehler als punktförmige Lichtquelle behandelt werden. Wir befinden uns für unsere Zwecke im euklidischen dreidimensionalen Raum mit geraden Wegen des Lichts und den einfachen Gesetzen der Geometrie bzw. Trigonometrie.
II. Erwartete Neigung der Mondsichel
1.) Im Folgenden wird zu Grunde gelegt, dass Mond und Sonne gleichzeitig am Himmel zu sehen sind. Das ist ab und zu der Fall, bei zunehmendem Mond nachmittags oder abends und bei abnehmendem Mond morgens. Als Beispiel soll angenommen werden, dass der Mond im Süden in einer Höhe von 40° und die Sonne im Westen in einer Höhe von 20° steht (das ist etwa im April oder im August möglich). Dann sähe der Betrachter die Sonne deutlich tiefer stehen als den Mond und würde erwarten, dass die Sichel eine negative Neigung hat und - in unserem Beispiel - nach rechts unten geneigt ist. Das wäre die erwartete Mondneigung. Diese lässt sich messen, konstruieren und berechnen.
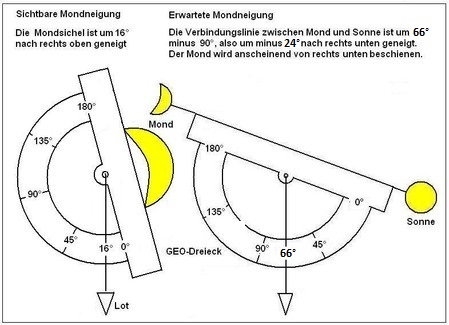
2.) Für die Messung kann der Betrachter die Mitte der (gedachten) Verbindungslinie zwischen Mond und Sonne suchen und dort mittels eines geeigneten Geräts (Geodreieck, Lot, siehe
Bild 2 a rechts) deren Neigung messen. Für bessere Genauigkeit sollte das Geodreieck senkrecht zur Blickachse gehalten, also etwas zum Betrachter hin gekippt werden. Für das in Zi. 1. genannte Beispiel - Mond im Süden mit 40° und Sonne im Westen mit 20° - würde man etwa messen, dass die vom Mond zur Sonne gehende Verbindungslinie um minus 24° (66° - 90°) nach rechts unten geneigt ist, siehe Bild 2 a, rechts. Diese Neigung würde man von der Sichel erwarten. Stattdessen sieht man, wenn man direkt auf den Mond blickt, dass seine Sichel keineswegs nach rechts unten, sondern mit plus 16° nach rechts oben geneigt ist, siehe Bild 2 a, links. (Zu den Messungen siehe auch unten zu III 4.)

3. Die geometrische und rechnerische Ermittlung der erwarteten Mondneigung ergibt sich gemäß der in Bild 3 hergeleiteten Formel. Dabei ist die Bildebene (anders in früheren Fassungen dieses Textes) gekippt, steht also ebenso senkrecht zur Blick-achse, wie das o.g. Geodreieck und wie die Bildebene in Bildern 4 mit 6. Wenn α die Höhe der Sonne, γ die des Mondes (beides gemessen z.B. mit dem kleinen, auf 1° genauen Sextanten von ASTRO-MEDIA) und β der absolute Wert ihrer Azimutdifferenz ist, lautet die Formel (Formel 1) für die erwartete Mondneigung α*:
α*(°) = grad {{ atan { 1/2 ( tan α - tan γ ) * cos β/2 : [ ( cos β/2 + 1/2 ( tan α + tan γ )) 2 ] 1/2 : sin β /2 } }}
Für obiges Beispiel würde man eine erwartete Mondneigung von minus 24° errechnen. Die gemessenen und errechneten Werte unterscheiden sich ggf. nur um Messfehler (dazu siehe auch unten zu III 4.)
III. Sichtbare Neigung der Mondsichel
1.) Die Neigung der Mondsichel, wie sie sich dem direkt auf den Mond gerichteten Blick zeigt (die sichtbare Mondneigung), lässt sich ebenfalls messen, konstruieren und errechnen. Gemessen wird sie so, wie Bild 2 a links das zeigt. Tatsächlich sieht und misst man, wenn man direkt auf den Mond blickt, die Sichel nicht, wie in unserem o.g. Beispiel erwartet, um minus 24° nach rechts unten, sondern mit 16° nach rechts oben geneigt. Der Grund dafür liegt nur in der Wirkung der Perspektive, die auf Seite D erläutert wird. Hier ist zunächst nur wesentlich, dass der Mond aus den oben unter I) 4.) genannten Gründen aus der gleichen Richtung beschienen wird, wie die Erde.
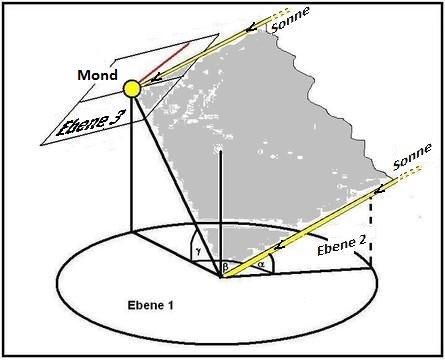
2.) In Bild 4 sind die zueinander parallelen, Erde und Mond treffenden Sonnenstrahlen mit gelben Linien dargestellt. Sie bestimmen, wenn die bis 5,2° betragende Abweichung der Mondbahn von der Ekliptik und wenn Bahnstörungen vernach-
lässigt werden, die Ekliptikebene, in der Mond und Erde gemeinsam um die Sonne kreisen - die grau getönte Fläche ist Teil dieser Ekliptikebene. Bei der geometrischen und rechnerischen Darstellung der sichtbaren Mondneigung sind die in Bild 4 zu sehenden drei Ebenen von Bedeutung. Ebene 1 ist die Horizontalebene des Betrachters. Ebene 2 wird durch die Schenkel der Sonnenhöhe α bestimmt. In Ebene 3, auf der die Blickrichtung senkrecht steht (die Bildebene), liegt der sichtbare Umkreis des Mondes, also der Großkreis, der die sichtbare von der unsichtbaren Mondhälfte trennt, und ebendort liegen die Spitzen der Sichel. Die den Mond treffenden Sonnenstrahlen liegen meist nicht in dieser Ebene 3, sondern schneiden sie, ähnlich wie der Zeiger der vertikalen Sonnenuhr vom Zifferblatt wegsteht.
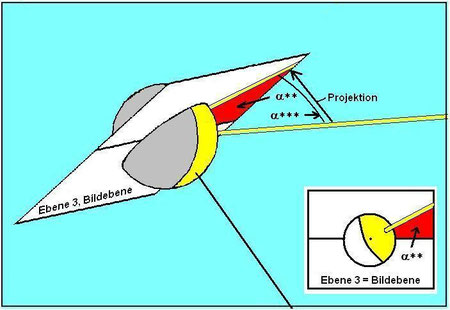
3.) Die sichtbare Neigung der Mondsichel ergibt sich, wenn der Winkel α, also die Sonnenhöhe, von Ebene 2 auf Ebene 3 projiziert wird. Ein Winkel verändert bei der Projektion auf eine zu ihm nicht parallele Fläche seine Größe. α wird also zu α**. In Bild 5 sind die Details zu sehen. Skizzen, Erläuterungen und Berechnungen analog zu den hier gegebenen Ableitungen finden sich auch in der im März 2010 erschienenen Arbeit von Prof. Dr. Glaeser und mir in KoG Nr. 13, S. 19 - 26.
Berechnet wird die sichtbare Neigung der Mondsichel gemäß der Skizze in Bild 6.
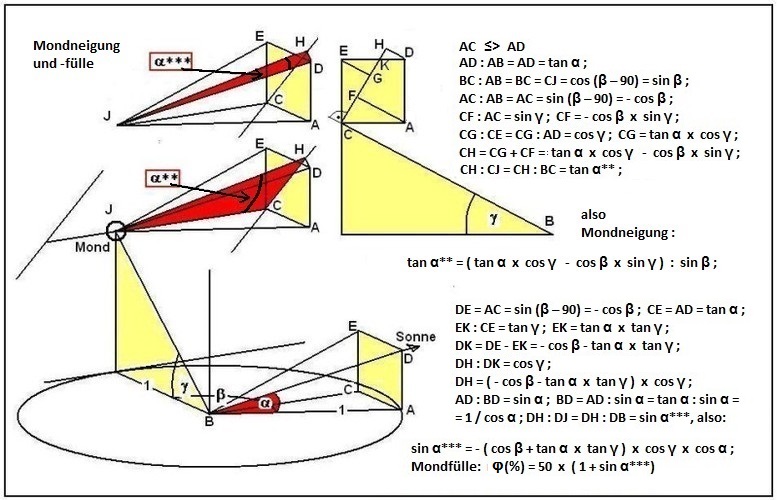
Die Formel (Formel 2) für die sichtbare Mondneigung α** lautet:
α**(°) = grad ( arctan ( ( tan α x cos γ - cos β x sin γ ) : sin β ) )
Für das in Zi. 1. genannte Beispiel ( Mond im Süden mit 40° und die Sonne im Westen mit 20° ) beträgt die so errechnete sichtbare Mondneigung plus 17° (die Sichel zeigt also nach oben, obwohl die Sonne tiefer steht).
4. Auch für die sichtbare Mondneigung sind die gemessenen und die errechneten Werte gleich groß bzw. unterscheiden sich ggf. nur um Messfehler. Eine andere, jedoch nicht ins Gewicht fallende Fehlerquelle ist die Lichtbrechung in der Atmosphäre, die tief, also nicht weit über dem Horizont stehende Gestirne etwas höher stehend erscheinen lässt, was sich bei der Mondneigung jedoch nicht bemerkbar macht. Weil die Entfernungen zwischen Sonne, Erde und Mond nicht Bestandteil der Formeln sind, wird die Genauigkeit der Ergebnisse auch nicht etwa dadurch gemindert, dass die Umlaufbahnen von Erde und Mond nicht genauen Kreisbahnen, sondern ellipsenähnlichen Bahnen entsprechen.
Die Abweichung der sichtbaren von der erwarteten Neigung der Sichel, die den Eindruck der "falschen" Mondneigung verursacht, entspricht der Differenz der beiden Neigungswerte, also dem Winkel δ, nämlich:
δ = α** - α*
Im o. g. Beispiel sind das für die errechneten Werte 17° minus minus 24°, und für die gemessenen Werte 16° minus minus 20°, also 41° bzw. 36° (!). Bei anderer Konstellation können sich Abweichungen von 60° und mehr ergeben. Mit einer optischen Täuschung kann das nicht erklärt werden.
IV. Mondphase
Die Stellung des Mondes zu Erde und Sonne bestimmt nicht nur die Neigung der Sichel, sondern auch die Phasen des Mondes (die Mondfülle, z. B. Voll-, Halbmond, seine früher so genannten "Lichtgestalten", deren Erklärung schon den alten Astronomen bekannt gewesen ist, siehe Brockhaus' Konversationslexikon, 14. Auflage, 1894-1896, Seite 989). Auch das Maß für die Mondphase φ kann aus den Winkeln α, β und γ gewonnen werden und wird ebenfalls in Bild 6 hergeleitet. Die Formel (Formel 3) lautet:
φ(%) = 50 x ( 1 - ( cos β + tan α x tan γ ) x cos γ x cos α )
φ ist eine Prozentzahl, die angibt, in welchem Verhältnis der beleuchtete Teil der Mondscheibe zum unbeleuchteten steht. 25 % entsprechen z. B. dem Viertelmond (die Sichel), 50 % dem Halbmond etc. Anstelle einer Prozentzahl wird die Mondphase oft auch in Grad angegeben, wobei 0° für den Neumond steht, 45° für die zunehmenden Viertelmond, 90° für den zunehmenden Halbmond, 180° für den Vollmond und 270° für den abnehmenden Halbmond. Auch die Formel hierfür ergäbe sich leicht aus Bild 6.
(Anmerkung: Die Formel für die Mondphase hatte ich zweimal fehlerhaft wiedergegeben. Den Hinweis für die Korrektur verdanke ich Herrn Dieter Schlagheck, der meine Formeln für Mondneigung und -phase in eine von ihm konstruierte astronomische Uhr integriert hat, beschrieben im Magazin Astronomie-Heute.de vom 15.05.08.
V. Werte aus dem Internet
Die eigenhändige Messung der Azimut- und Höhenwerte oder ihre Bestimmung anhand der Ephemeriden kann man sich ersparen.
Die Werte lassen sich für beliebige Zeitpunkte und Standorte aus dem Internet holen. Sogar die Neigung der Mondsichel findet man dort, und zwar für die je aktuelle Tageszeit und
für jeden Ort bei dem sehr guten Internetdienst "Wolfram Alpha", allerdings nur als
Abbildung, aus der man den Winkel aber durch Ausmessen entnehmen kann. Die Mondphase ist dagegen sowohl abgebildet als auch mit einem Wert
angegeben. Aus all dem ersieht man übrigens, dass der geometrische Zusammenhang zwischen Mondneigung und -phase und Azimut und Höhe von Sonne und Mond keineswegs meine Entdeckung ist; er liegt
z.B. den Angaben des
Internetdiensts Wolfram Alpha zugrunde. Der Zusammenhang ist eine Selbstverständlichkeit und eine geometrische Banalität, ebenso wie die "falsche" Mondneigung eine perspektivische
Banalität ist (siehe nächste Seite).
VI. Mondneigung und Mondbahn
Es gibt eine im Internet geäußerte, jedoch unzutreffende Vermutung (siehe Seite E, Zi. 5.), wonach die Symmetrieachse der Mondsichel die Tangente an die Bahnkurve des Mondes ist.

Bild 6 a gibt die Vermutung wieder. Ihr zufolge dürfte die Mondneigung nicht vom Stand der Sonne abhängen. Dass das nicht zutreffen kann, zeigt Formel 2 . Denn Höhe und Azimut der Sonne sind Bestandteil der Formel. Der Stand der Sonne hat daher Einfluss auf die Neigung der Sichel. Die Vermutung trifft nicht zu. Manchmal ist die Abweichung groß. Manchmal gibt es eine Annäherung der Werte. Eine Differenz verbleibt jedoch immer.
